
Effect of Ideal Filtering:
The Inverse Fourier transform of Y(w) = X(w) for
|w| < W,
and Y(w) = 0 for |w| > W is
y(t) =
(1/2p) -W/|/WX(w)e
jwtdt
Therefore the time signal corresponding to the ideal filtered spectra
|Y(w)| = |X(w)| for |w| < W,
|Y(w)| = 0 for |w| >W
<Y(w) = <X(w) for |w| < W,
<Y(w) = 0 for |w| > W
is related to x(t) in a rather complicated way.
Compare the magnitude spectrum of X(w) with the
filtered magnitude spectrum of Y(w)
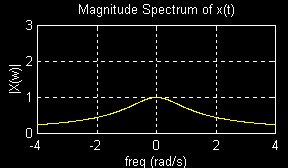

and the phase spectrum of X(w) with the filtered phase
spectrum of Y(w)
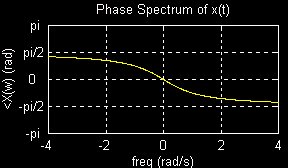

to the corresponding time signals
x(t) = e-tu(t)
y(t) =
(1/2p)
-W/|/WX(w)ejwtdt
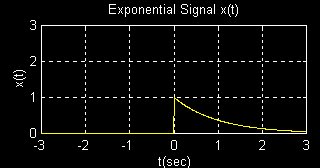

 return to Magnitude and Phase Spectra page
return to Magnitude and Phase Spectra page







