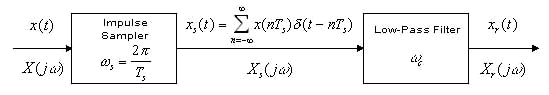
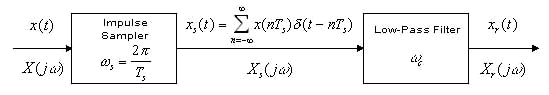
A continous-time signal x(t) is sampled at a frequency of
ws rad/sec. to
produce a sampled signal xs(t).
We model xs(t) as an impulse
train with the area of the nth impulse given by
x(nTs ). An ideal low-pass
filter with cutoff frequency wc
rad/sec. is used to obtain the reconstructed signal
xr(t).
Suppose the highest-frequency component in x(t) is at frequency wm. Then the Sampling Theorem states that for ws > 2wm there is no loss of information in sampling. In this case, choosing wc in the range wm <wc <ws - wm gives xr(t) = x(t). These results can be understood by examining the Fourier transforms X(jw), Xs (jw), and Xr(jw). If ws <2 wm and/or wc is chosen poorly, then xr(t) might not resemble x(t).
To explore sampling and reconstruction, select a signal or use the mouse to draw a signal x(t) in the window below. After a moment, the magnitude spectrum |X(jw)| will appear. Then, enter a sampling frequency ws and click "Sample" to display the sampled signal and its magnitude spectrum. Finally, choose a cutoff frequency wc and click "Filter." The reconstructed signal and its magnitude spectrum will be shown.
|
Applet by Steve Crutchfield.
|