Drilling for oil:
This is a problem of inferring a hidden surface--in this case a layer of oil-bearing shale--from a series of test wells. The drilling of each well has an associated cost, and the object is to determine the underlying shale surface for the least cost. The cost of drilling is as follows:
$500 for each well +
$1/ft depth +
$500 (if well is drilled in water) +
$500 (if well is drilled in swamp)
Possible surfaces are:
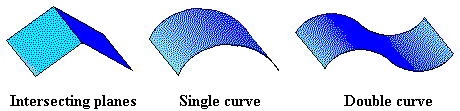
Each of these surfaces may occur inverted (e.g., the "single curve" may be concave or convex upwards); each may be tilted with respect to the horizontal; and each may be rotated with respect to the vertical.
Your assignment is to determine the surface type, its orientation with respect to North, and the direction of tilt--if any. Note that each of these surfaces is a "ruled surface", i.e., each can be swept out by a straight line. It is the orientation and direction of tilt of this straight line that should be reported. A sufficient answer would be "intersecting planes, concave upwards, running NW to SE, tilting down toward the SE".
When you are convinced you know the underlying surface, click on the button PRESS WHEN DONE to terminate your drilling. Then, the use "print screen" to capture your work. This captured image should be incorporated in your writeup of this project. Cost is important, but getting the right answer is more important. Make sure you've sunk enough wells to be pretty confident about your conclusions.
This problem can be run two ways: from a flat plain (with no interesting features like hills, lakes, and swamps), or from real topography (with all of the above). It's OK to work just with the flat topography. But if you're brave (and want extra credit) try the hilly topography. Here you'll have to subtract out the topographical features to deduce the underlying stratum, because the well depths are listed as the distance from the surface to the underlying stratum.
Note: Be careful in translating the x-y coords into compass directions because in this computer simulation x increases left to right, but y increases from top to bottom.
Choose problem type: